Training A Model (For Supervised Learning)
Holdout method
A model is trained using labelled input data in the case of supervised learning. However, how can we comprehend the model's performance? The test results may not be available right away. Furthermore, the label value of the test data is unknown. That is why a portion of the input data is held back (hence the name holdout) for model evaluation. This subset of input data is used as test data to assess the performance of a trained model. In general, 70%—80% of the input labelled data is used for model training. The remaining 20%—30%is used as test data for validation of the performance of the model. However, a different proportion of dividing the input data into training and test data is also acceptable. To make sure that the data in both the buckets are similar in nature, the division is done randomly. Random numbers are used to assign data items to the partitions.
This method of partitioning the input data into two parts — training and test data which is by holding back a part of the input data for validating the trained model is known as holdout method.
Once the model is trained using the training data, the labels of the test data are predicted using the model's target function. Then the predicted value is compared with the actual value of the label. This is possible because the test data is a part of the input data with known labels. The performance of the model is in general measured by the accuracy of prediction of the label value.
In certain cases, the input data is partitioned into three portions —a training and a test data, and a third validation data. ne validation data is used in place of test data, for measuring the model performance. It is used in iterations and to refine the model in each iteration. The test data is used only for once, after the model is refined and finalized, to measure and report the final performance of the model as a reference for future learning efforts.
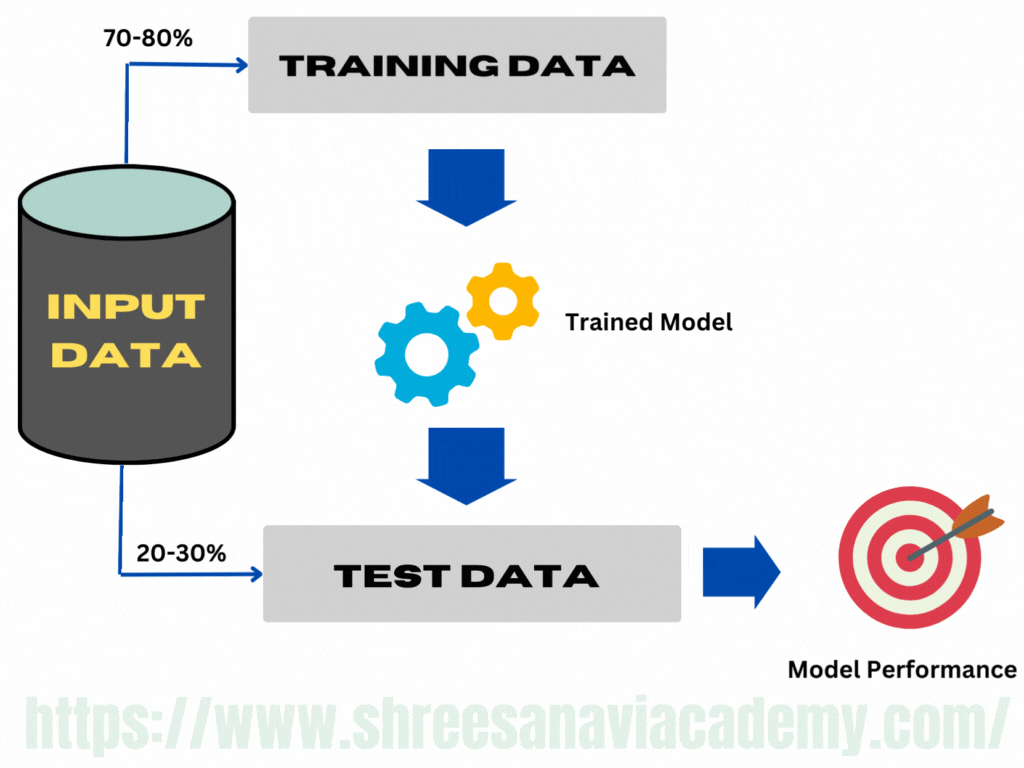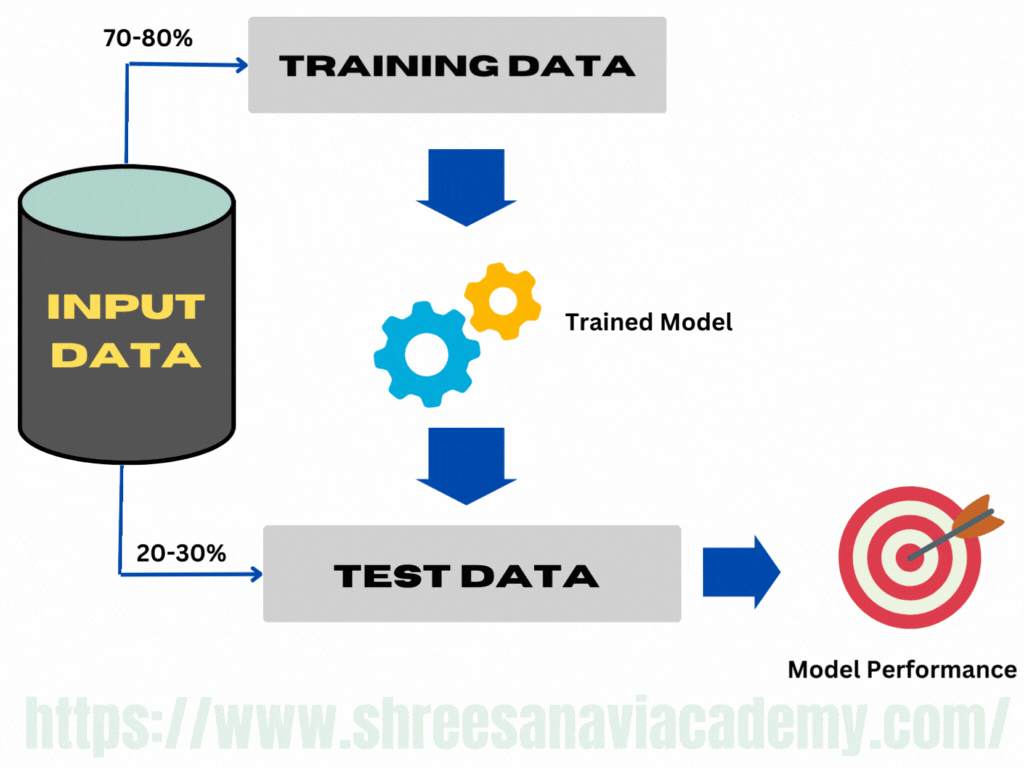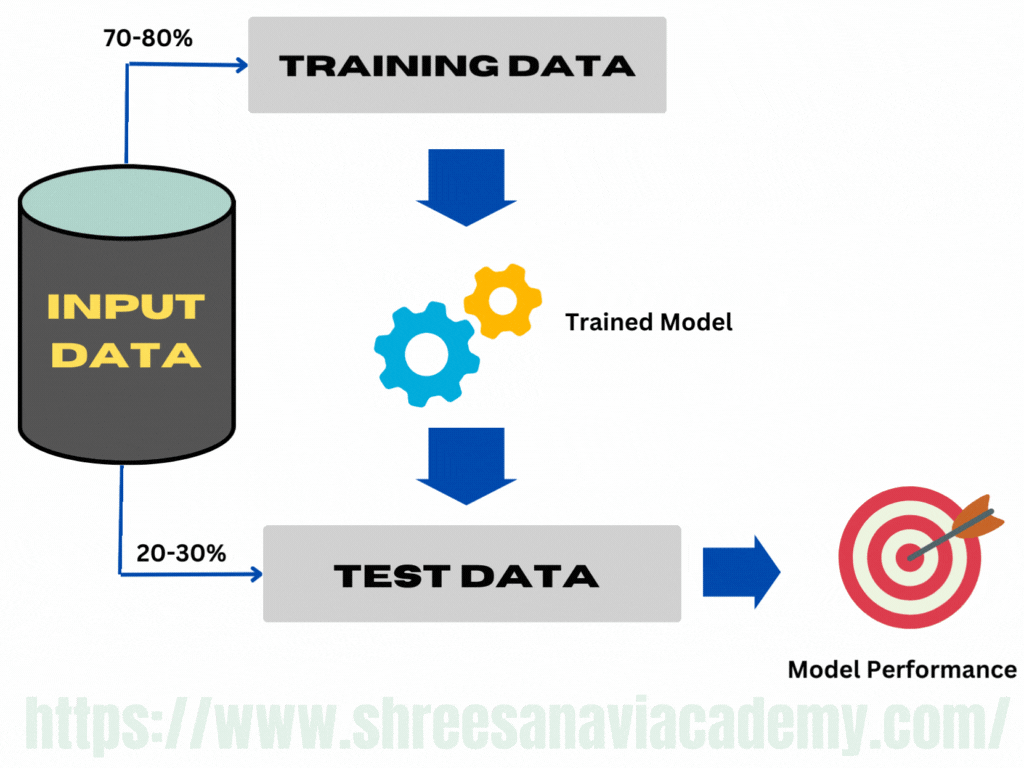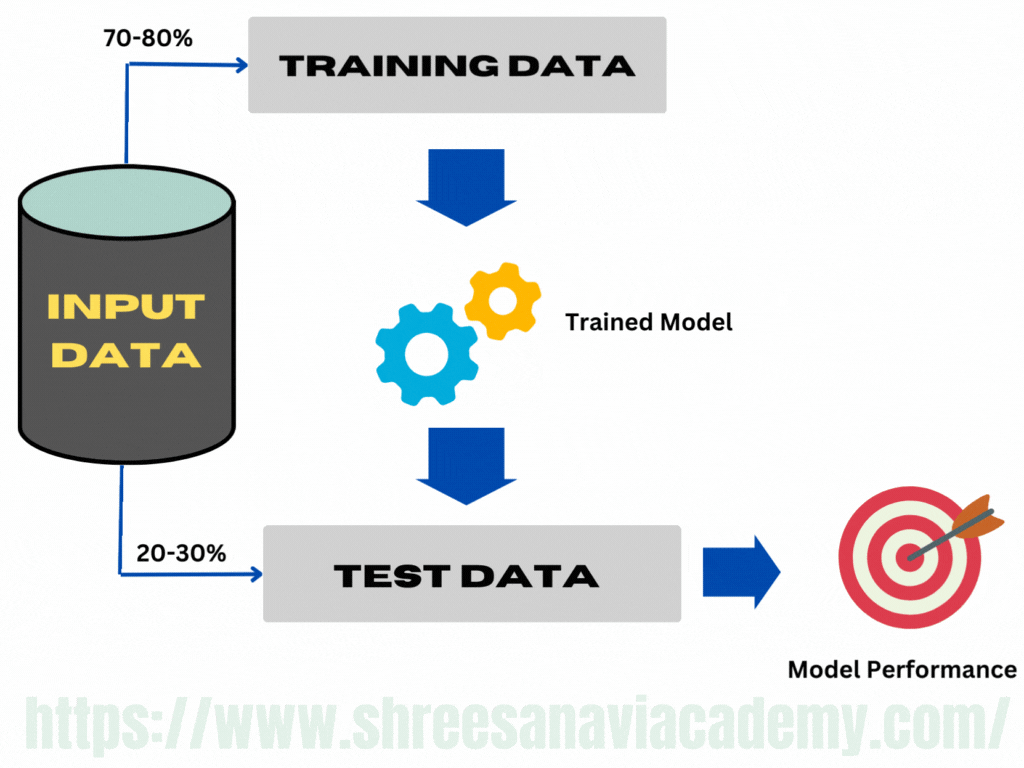
Figure: Holdout method
An obvious problem in this method is that the division of data of different classes into the training and test data may not be proportionate. This situation is worse if the overall percentage of data related to certain classes is much less compared to other classes. This may happen despite the fact that random sampling is employed for test data selection. This problem can be addressed to some extent by applying stratified random sampling in place of sampling. In case of stratified random sampling, the whole data is broken into several homogenous groups or strata and a random sample is selected from each such stratum. This ensures that the generated random partitions have equal proportions of each class.
K-fold Cross-validation method
Holdout method employing stratified random sampling approach still heads into issues in certain specific situations. Especially, the smaller data sets may have the challenge to divide the data of some of the classes proportionally amongst training and test data sets. A special variant of holdout method, called repeated holdout, is sometimes employed to ensure the randomness of the composed data sets. In repeated holdout, several random holdouts are used to measure the model performance. In the end, the average of all performances is taken. As multiple holdouts have been drawn, the training and test data (and also validation data, in case it is drawn) are more likely to contain representative data from all classes and resemble the original input data closely. This process of repeated holdout is the basis of k-fold cross-validation technique. In k-fold cross-validation, the data set is divided into k-completely distinct or non-overlapping random partitions called folds.
The value of 'k' in k-fold cross-validation can be set to any number. However, there are two approaches which are extremely popular:
(i) 10-fold cross-validation (10-fold CV)
(ii) Leave-one-out cross-validation (LOOCV)
10-fold cross-validation is by far the most popular approach. In this approach, for each of the 10-folds, each comprising of approximately 10% of the data, one of the folds is used as the test data for validating model performance trained based on the remaining 9 folds (or 90% of the data). This is repeated 10 times, once for each of the 10 folds being used as the test data and the remaining folds as the training data
Bootstrap sampling
Bootstrap sampling, also known as bootstrapping, is a popular method for identifying training and test data sets from an input data set. It employs the Simple Random Sampling with Replacement (SRSWR) technique, which is a well-known sampling theory technique for generating random samples. We have seen earlier that k-fold cross-validation divides the data into separate partitions —say 10 partitions in case of 10-fold cross-validation. Then it uses test data from the partition and training data from the remaining partitions. Unlike the approach used in k-fold cross-validation, bootstrapping selects data instances at random from the input data set, with the possibility of selecting the same data instance multiple times. This essentially means that bootstrapping can generate one or more training data sets with 'n' data instances from the input data set, with some of the data instances repeated multiple times. This technique is especially useful with small input data sets, i.e. with a small number of data instances.