Model Representation and Interpretability
We have already seen that the goal of supervised machine learning is to learn or derive a target function which can best determine the target variable from the set of input variables. A key consideration in learning the target function from the training data is the extent of generalization. This is because the input data is just a limited, specific view and the new, unknown data in the test data set may be differing quite a bit from the training data.
Fitness of a target function approximated by a learning algorithm determines how correctly it is able to classify a set of data it has never seen.
Underfitting
If the target function is too simple, it may be unable to capture the essential nuances and accurately represent the underlying data. A typical case of underfitting occurs when attempting to represent non-linear data with a linear model, as illustrated by the two cases of underfitting shown in the figure below. Underfitting is frequently caused by a lack of sufficient training data. Underfitting causes both poor performance with training data and poor generalisation to test data. Underfitting can be avoided by
1. using more training data
2. reducing features by effective feature selection
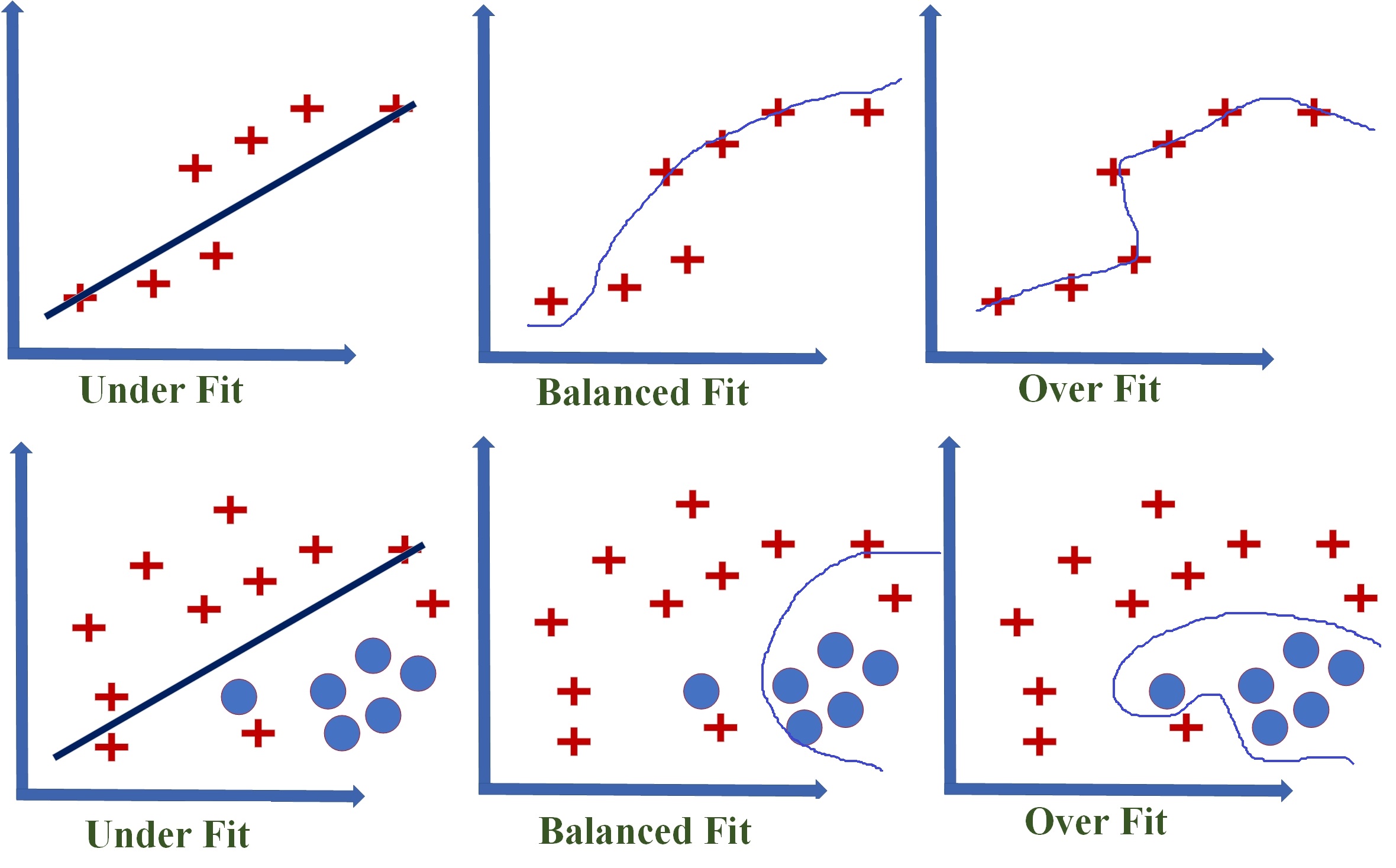
Figure: Underfitting and Overfitting of Models
Overfitting
Overfitting occurs when the model is designed in such a way that it closely mimics the training data. Any specific deviation in the training data, such as noise or outliers, is then embedded in the model. It has a negative impact on the model's performance on the test data. Overfitting occurs frequently as a result of attempting to fit an overly complex model to closely match the training data. In these cases, the target function attempts to ensure that all training data points are correctly partitioned by the decision boundary. However, this exact nature is not always replicated in the unknown test data set. As a result, the target function causes incorrect classification in the test data set. Overfitting produces good results with the training data set but poor generalisation and thus poor performance with the test data set. Overfitting can be avoided by
1. Using re-sampling techniques like k-fold cross validation
2. Hold back of a validation data set
3. Remove the nodes which have little or no predictive power for the given machine learning problem.
Both underfitting and overfitting result in poor classification quality which is reflected by low classification accuracy.
Bias-Variance trade-off
In supervised learning, the class value assigned by the learning model built based on the training data may differ from the actual class value. This error in learning can be of two types —errors due to 'bias' and error due to 'variance'. Let's try to understand each of them in details.
Errors due to 'Bias'
Bias errors result from the model's simplifying assumptions in order to make the target function less complex or easier to learn. In short, it is due to the model's underfitting. Because metric models are generally biassed, they are easier to understand/interpret and learn faster. These algorithms perform poorly on data sets that are complex in nature and do not align with the algorithm's simplifying assumptions. Underfitting leads to a high level of bias.
Errors due to 'Variance'
Variance errors result from differences in the training data sets used to train the model. To train the model, different training data sets (randomly sampled from the input data set) are used. The difference in the data sets should ideally be negligible, and the model trained using different training data sets should not be too dissimilar. In the case of overfitting, however, because the model closely matches the training data, even minor differences in the training data are magnified in the model.
So, the problems in training a model can either happen because either (a)the model is too simple and hence fails to interpret the data grossly or (b) the model if extremely complex and magnifies even small differences in the training data.
As is quite understandable:
• Increasing the bias will decrease the variance, and
• Increasing the variance will decrease the bias
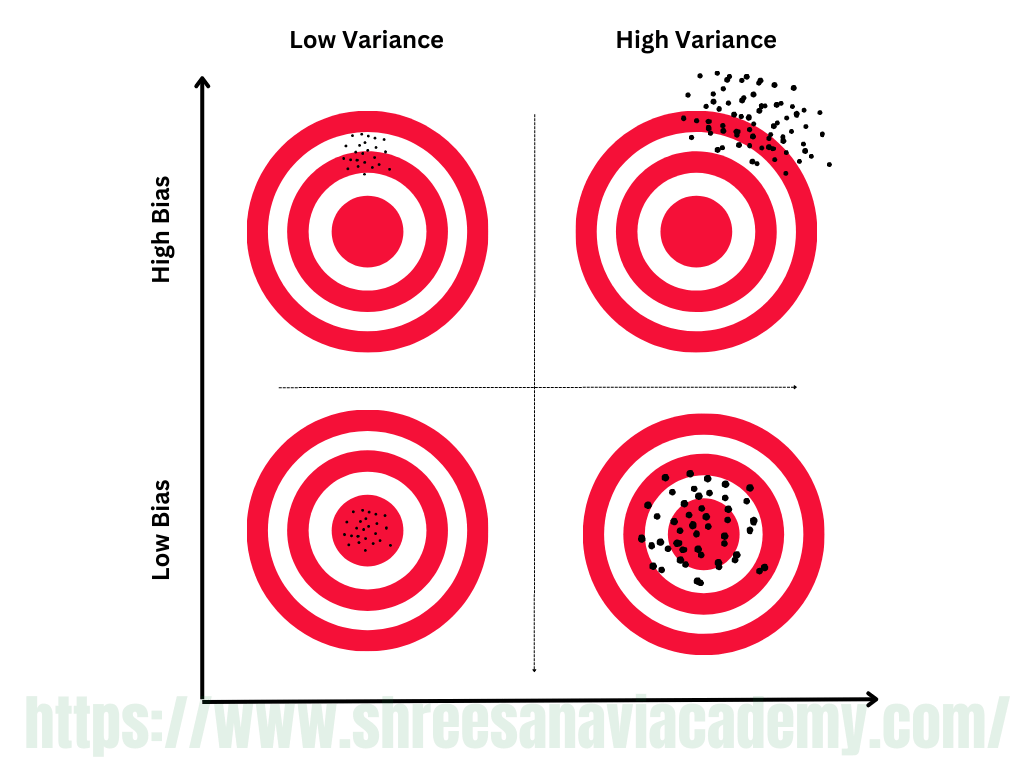
Figure: Bias-Variance Trade-off